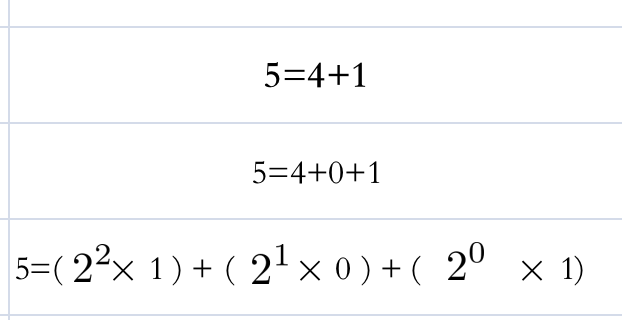二进制
二进制计算
计算机的世界里缺少不了二进制的存在，我们总听到计算机是 0 和 1 组成的，而这两个数字恰恰就是二进制的必备元素
十进制与二进制
十进制：回到小学初识数字的时候，从小到大接触的数字中从 0 数到 9，比 9 大一个数就要进一位也就是 10，这就是十进制，即逢 10 进 1，这就是十进制
二进制：从 0 开始数，当数到 2 时就进一位，即逢 2 进一，例如： 0，1，10，11，100，101，110,111。这就是二进制
转换
初次接触二进制总会觉得别扭，例如 101，这个数字在十进制中是一百零一，在二进制中他就代表了数字 5，这时候脑袋上可能会有大大的问号，怎么就知道他就是 5 呢，这里就要说一下进制转换了
当我们已知一个十进制数字的时候怎么转换成二进制呢，（余数法）方法如下：
- 5 ÷ 2 = 2 … 1
- 2 ÷ 2 = 1 … 0
- 1 ÷ 2 = 0 … 1
我们从上到下将余数拼接就是 5（十进制）= 101（二进制）
如果这里还是没看懂那可以看接下来的解释
我们从 0 开始数（下面示例中序号为十进制，计算为二进制）
- 0
- 0 + 1 = 1
- 1 + 1 = 10 (二进制)，二进制逢 2 进 1，此处进位即 10 (二进制)
- 10 + 1 = 11
- 11 + 1 = 100，二进制逢 2 进 1，进位后为 20，同理进位即 100
- 100 + 1 = 101
进阶
熟练转换以后我们可以把二进制和十进制做一个对比：
将二进制中只有 1 和 0 的情况提取出来，就行成了下面这样：
这个时候把列表反过来看：
把这个对照变成二进制再看一下：
回过头再看一下最一开始的例子即 5 (十进制) 转换为二进制 101：
以上就是十进制转二进制全过程了
而二进制转换十进制就是将表中对应的数字上下相乘，然后结果相加即可
字节
在计算机系统中 字节 (byte) 是最基础的计量单位，一个字节代表了一个 8 位长的二进制数字，每四个字节拼在一起代表了一个字
简单标识就是如下面原码所示，00000000 这个八个数字组成一个字节，四个字节组成了一个数字 5，即
00000000 00000000 00000000 00000101
原码
原码：即原数字转换为二进制后的二进制数
5 的原码为
00000000 00000000 00000000 00000101
反码
反码：反码即对原码进行取反，将所有的 0 换为 1，所有的 1 换为 0
5 的反码为
11111111 11111111 11111111 11111010
补码
补码：补码是反码 + 1
所以上述的补码为
11111111 11111111 11111111 11111010 + 1 =
11111111 11111111 11111111 11111011
补码在二进制中主要表示一个整数的负数
