数据结构–线性表

⚠️ 本文中代码均使用 C++ 进行编码

线性表是线性数据结构的典型代表，线性表是一种最基本、最简单的数据结构，数据元素之间仅具有单一的前驱和后继关系。线性表不仅有着广泛应用，同时它也是其他数据结构的基础。

线性表简称表，是n(n>=0)个具有相同数据类型的数据元素的有限序列，线性表中数据元素的个数称为线性表的长度，长度等于零时称为空表

我们通常使用ai表示线性表中的第i个元素，而a1也就是线性表的第一个元素，他没有前驱，而an则是线性表的最后一个元素，他没有后继，其他每个元素仅有一个前驱和一个后继

线性表中一般都包含一下的方法或操作，以供我们对线性表进行各种操作：

  • Data(用于存储数据)
  • InitList（创建一个新的空的线性表）
  • DestoryList（销毁线性表并释放空间）
  • Length（获取线性表长度，记线性表中元素的个数）
  • Get（获取线性表中第i个位置的元素）
  • Locate（按值查找，返回该值所对应的位置序号）
  • Insert（向位置i插入元素x）
  • Delete（删除线性表中位置i所对应的元素）
  • Empty（判空操作，返回一个bool值，判断线性表是否为空）
  • PrintList（对线性表进行遍历操作，依次输出线性表元素）

顺序表

线性表中的顺序存储结构叫做顺序表

顺序表是使用一段地址连续的存储单元一次储存线性表的数据元素。

由于数据表中元素类型相同，且按照一定顺序进行存储，因此我们一般使用数组来实现顺序表，这也就导致了数据元素的序号与数组下标形成了一一对应的关系。

但是由于使用数组进行存储，也就引出了一系列的问题，其中最主要的就是，我们使用数组来对顺序表进行实现，那么我们在定义顺序表时就需要给行顺序表的长度，当我们要进行增加元素操作时就需要向系统申请新的空间，而且因为使用了数组，而数组场读固定，我们通常会进行顺序表的插入、删除等操作，我们也就需要将数组的长度设置大于顺序表的长度即MaxSize > length

此处添加示意图

设顺序表的每个元素占用c个存储单元，则第i个元素的存储位置为：

LOC(ai) = LOC(a1) + (i - 1) × c

实现

由于元素类型是不确定的，因此在这里使用C++的模板机制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const int MaxSize = 100;
template <class DataType> class SeqList {
    public:
    	SeqList() {length = 0;} 		//无参构造函数
    	SeqList(DataType a[], int n); 	//有参构造函数
    	~SeqList() {} 					//析构函数
    	int Length() {return length;} 	//获取线性表长度
    	DataType Get(int i);			//按位查找，第i个元素
    	int Locate(DataType x); 		//按值查找，返回序列号
    	void Insert(int i, DataType x); //插入操作，在第i个位置插入值x
    	DataType Delete(int i); 		//删除操作，删除第i个位置的元素
    	void PrintList(); 				//遍历操作，依序输出整个顺序表
    private:
    	Datatype data[MaxSize]; 		//存放数据元素的数组
    	int length;						//线性表的长度

构造函数

  • 无参构造： 只需要简单地将顺序表的长度length初始化为0
  • 有参构造： SeqList(DataType a[], int n);需要传入长度n以创建一个长度为n的顺序表，需要将传入的数组元素作为线性表的数据元素传入顺序表，并将传入元素的个数作为顺序表的长度
    1
    2
    3
    4
    5
    6
    7
    template <class DataType> SeqList::SeqList(DataType a[], int n) {
        if(n > MaxSize) throw "非法参数";
        for(int i = 0; i < n; i++) {
            data[i] = a[i];
        }
        length = n;
    }

查

  1. 按位查找

    顺序表中第i个元素，对应数组中的下标为i-1，所以顺序表只需要一次遍历就能查找到对应位置的元素，时间复杂度即为O(1)

    1
    2
    3
    4
    template <class DataType> DataType SeqList::Get(int i) {
        if(i < 1 && i > length) throw "查找位置非法";
        else return data[i-1]
    }

  2. 按值查找

    值查找的方法就是简单粗暴了，直接一次遍历，对比所有值，找到所需要元素，然后返回其序号（不是下标），如果不成功则返回失败标志“0”

    1
    2
    3
    4
    5
    6
    7
    8
    9
    template <class DataType>
    int SeqList::Locate(DataType x)
    {
        for(int i = 0; i < length; i++) {
            if(data[i] == x)
                return i+1;
        }
        return 0;
    }

    按值查找的平均时间性能也是O(n)，因为我们只需要进行一次循环遍历，即时对比，就能轻易找到答案

增

顺序表的增加操作应该是所有线性表操作中最麻烦的，因为涉及到顺序表的长度问题，当我们在第i个位置插入一个新元素x，则线性表长度从n变为n+1

插入算法的逻辑基本上是这样的：

  • 当需要插入的位置位于末尾时，我们仅需要修改顺序表长度，并且将元素添加在末尾就可以了
  • 当需要插入的元素不在末尾时，我们则需要逆序遍历整个顺序表，将所有的元素向后挪动一个位置，直到我们需要插入元素的第i个位置，然后将元素插入，最后将顺序表的长度+1即可
  • 如果插入元素的位置不合理或表满了，那么就抛出错误即可 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    template <class DataType> 
    void SeqList::Insert(int i, DataType x)
    {
        if(length >= MaxSize) throw "上溢";
        if(i < 1 || i  length + 1) throw "插入位置错误";
        for(int j = length; j >= i; j++) { //数组最后一个存储位置为length - 1
            data[j] = data[j-1];
        }
        data[i-1] = x;
        length ++;
    }
  • 当元素在表尾时(i = n+1)，元素不需要后移，时间复杂度为O(1)
  • 当元素在表头时(i = 1)，元素需要移动n次，这是最坏的情况，时间复杂度为O(n)
  • 当元素在其他位置时，元素需要移动的平均时间复杂度为O(n)

删

顺序表中的删除操作，需要将指定位置的元素删除，并且将指定位置之后的元素全部前移，且删除操作的时间复杂度与增加操作基本一致

1
2
3
4
5
6
7
8
9
10
11
template <class DataType>
DataType SeqList::Delete(int i){
    if(length == 0) throw "下溢";
    if(i < 1 || i > length) throw "删除位置错误";
    x = data[i - 1];
    for(int j = 1; j < length; j ++) {
        data[j - 1] = data[j];
    }
    length --;
    return x;
}

遍历

遍历就更简单了，直接依序输出所有元素就可以了：

1
2
3
4
5
6
template <class DataType>
void SeqList::PrintList() {
    for(int i = 0 ; < length; i++)
        cout<" ";
    cout<<endl;
}

链表（Linked List）

顺序表利用了数组元素在物理上的位置的邻接关系来表示线性表元素之间的逻辑关系，拥有不少优点的同时也反映出了很多的缺点：

  • 插入和删除操作都需要进行大量的移动
  • 顺序表的容量固定，长度必须事先设定，但是如果需要存储的元素未知个数就无法确定长度了
  • 造成存储空间的“碎片”，数组要求占用连续的存储空间，即使存储单元数超过所需的数目，如果不连续也不能使用，造成空间的“碎片”现象

解决上述问题，最根本的原因其实就是静态资源分配，因此为了解决这些问题，我们可以使用链式存储来进行动态的资源分配

链表的基础实现方式很简单，就是使用任意的存储空间，对链表元素进行存储，在每一个链表结点中都存储一个指向下一个结点的指针，以便形成逻辑上的链式存储结构

单链表

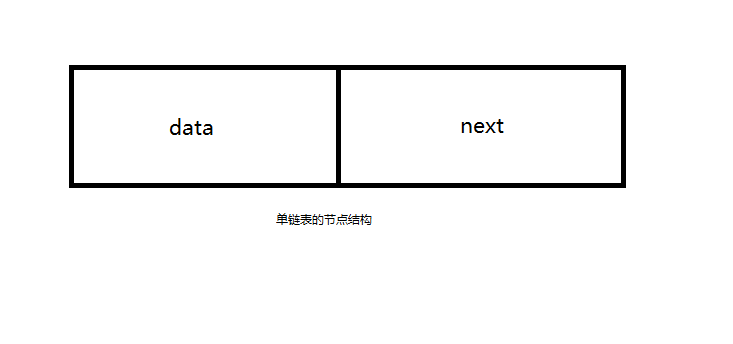
单链表就是用一组任意的存储单元存放线性表的元素，这组存储单元可以连续，也可以不连续，但是为了确定元素之间的逻辑关系，在存储数据的同时，必须存储其后继元素所在的地址信息，而这个存储单元被称为结点

data是数据域，用以存储数据元素，next是指针域（也称链域），用来存储后继结点的地址

由于元素类型不确定，下面的所有代码中均默认元素为int类型

结点的定义如下：

1
2
3
4
5
6
7
typedef bool Boolean;
typedef int DataType;
typedef struct Node
{
	DataType data; //数据域
	struct Node *next; //指针域
}node, *pnode;

为了我们能够轻易地找到链表，且因为第一个元素无前驱，我们必须对链表设置头指针指向第一个元素所在的结点；因为最后一个元素无后继，所以最后一个结点的next指向为NULL

单链表的方法定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class LinkList
{
public:
	int size;  	//链表长度
	pnode head; //pnode是Node类型的指针
public:
	
	LinkList(); 					//无参构造函数
    LinkList(DataType a[], int n);  //有参构造函数
	~LinkList();					//析构函数
	Boolean Insert(DataType, int);  //插入函数
	Boolean Del(DataType); 			//删除函数
	Boolean IsEmpty();				//判空函数
	int Locate(DataType x);			//按值查找函数	
    DataType Get(int i);			//按位查找函数
	void PrintList(); 				//遍历函数
};

下面的方法实现顺序从易到难，可能并不按照上述方法定义的顺序。

构造与析构

与顺序表不同，链表的构造函数中我们需要对头结点进行创建操作

1
2
3
4
5
6
LinkList::LinkList()
{
	head=new node; 	//创建head为node结点
	head->next=NULL;//使head的next指针指向为空
	size=0;			//初始化长度为0;
}

有参构造函数：

  1. 头插法

    头插法就是每次都将新申请的结点插入到头结点的后面

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    LinkList::LinkList(DataType a[], int n) {
        head = new node;
        head->next = NULL;
        size = 0;
        for(int i = 0; i < n; i ++) {
            pnode s;
            s = new node;
            s->data = a[i];
            s->next = head->next;
            head->next = s;
            size++;
        }
    }

  2. 尾插法

    尾插法就是将每一个新申请的结点插入到终端结点的后面，将终端结点的next指向新结点，将新结点作为插入后的终端结点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    LinkList::LinkList(DataType a[], int n) {
        head = new node;
        p = head;
        for(int i = 0; i < n; i ++) {
            pnode s;
            s = new node;
            s->data = a[i];
            p->next = s;
            p = s;
            size++;
        }
        p->next = NULL;//创建完毕后直接将尾结点的next指针赋空
    }

析构函数的作用的释放空间，因此我们需要对链表进行从头至尾的释放：

1
2
3
4
5
6
7
8
9
10
11
LinkList::~LinkList()
{
	pnode pn;
	pn=head;
	while(pn!=NULL)
	{
		head=head->next;
		delete pn;
		pn=head;
	}
}

遍历

其实遍历的方式与上面的析构函数中的实现方式基本一致，从我们定义的头结点开始，判断next指针是否为空，若为空则证明链表遍历完毕，若不为空，则将遍历指针移动到next指向的结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void LinkList::Print()
{
	if(IsEmpty())
	{
		cout<<"This List is empty"<<endl;
	}
	else
	{
		pnode pn;
		pn=head->next;
		while(pn!=NULL)
		{
			cout<data<<" ";
			pn=pn->next;
		}
		cout<<endl;
	}
}

判空

判空函数十分简单，直接上代码

1
2
3
4
5
6
Boolean LinkList::IsEmpty()
{
	if(size==0)
		return true;
	return false;
}

查

查找操作一共分为两种，按值查找（Locate）和按位查找（Get）

  1. 按值查找

    按值查找就是给定一个值去查找它在链表中的位置，实现方式也是从头结点head开始逐一对比，找到即返回位置

    由于需要逐一对比，所以在等概率的情况下，平均时间性能为O(n)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    int LinkList::Locate(DataType ele)
    {
      if(IsEmpty())
      {
        cout<<"Error :This List is empty!"<<endl;
        return -2;
      }
      int index=0;
      pnode inode;
      inode=head;
      while(inode!=NULL)
      {
        if(index!=0)
        if(inode->data==ele){
                cout<<"index:"<endl;
                return index;
                break;
            }
        inode=inode->next;
        index++;
      }
      cout<<"The number is not in this list!"<<endl;
      return -1; //未搜到
    }

  2. 按位查找
    按位查找就是给定一个位置，然后对链表进行遍历，找到对应位置的元素返回即可

    若查找位置位i则需要执行对比i-1次，等概率情况下，平均时间性能为O(n)，因此单链表是顺序存取

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    DataType LinkList::Get(int i) {
        if(IsEmpty())
      {
        cout<<"Error :This List is empty!"<<endl;
        return -2;
      }
        p = head->next;
        int count = 1;
        while(p != NULL && count < i) {
            p = p-> next;
            count ++;
        }
        if(p == NULL) {
            cout<<"位置错误"<<endl;
        } else {
            return p -> data;
        }
    }

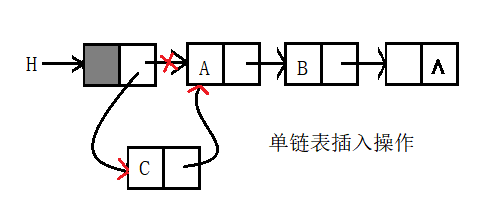
插入

链表的插入操作相对于顺序表要容易很多，因为是链式结构只需要处理相邻元素即可，不会影响整个线性表，这也是链表相对顺序表最大的优点之处

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Boolean LinkList::Insert(DataType ele,int loc) //数据、插入位置
{
	if(loc < 0 || loc > size) //判断位置是否合法
	{
		cout<<"Location is invalid."<<endl;
		return false;
	}
	int i,index=0;
	pnode inode,snode,erg;
	snode=new node;
	snode->data=ele;
	inode=head;
	erg=head;
	if(loc==size)//插入位置在结尾位置
	{
		while(inode->next!=NULL) 
		{
			inode=inode->next;
		}
		snode->next=inode->next;
		inode->next=snode;
	}
	else //插入位置非结尾位置
	{
		for(i=0;i<=loc;i++) //搜寻指定位置
		{
			inode=inode->next; //head -> next
			if(i!=0)//错位，erg需要在inode前一个结点
				erg=erg->next; //head ->next
			index++;
		}
		snode->next=inode;  //插入操作
		erg->next=snode;
	}
	size++; //插入后修改size
	return true;
}

删除

删除操作的主要时耗也是在查找正确的删除位置上，因此时间复杂度为O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Boolean Linear::Del(DataType ele)
{
	pnode inode,snode;
	int i,loc=0;
	inode=head;
	loc=Search(ele);
	if(loc==-2)return false;
	if(loc==-1)
	{
		cout<<"CON'T DELETE : This number is not in this list!"<<endl;
		return false;
	}

	for(i=0;i-1;i++) //查找需要删除结点位置
	{
		inode=inode->next;
	}
	if(loc==size) // 如果要删除的结点在尾部
	{
		snode=inode->next;
		inode->next=NULL;
		delete snode; //释放空间
	}
	else
	{
		snode=inode->next;
		inode->next=snode->next; //跳过snode指向的结点，将inode指向inode的下下个结点
		delete snode;//释放空间
	}
	size--;
	return true;
}

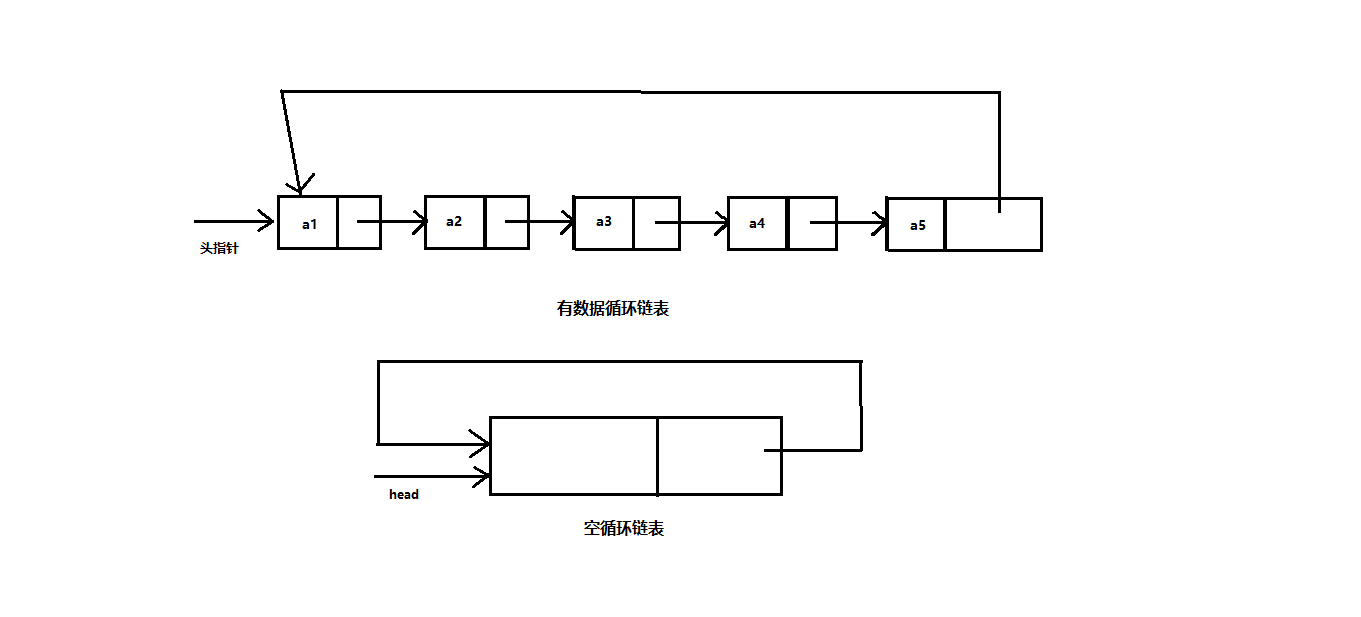
循环链表

循环链表的原理其实就是没有尾结点，将逻辑上的尾结点的next指针直接指向head头结点，形成逻辑循环链表

双链表

双链表与单链表的区别就是结点除了有用指向后继结点的next以外，还会存在prior的指向前置结点的指针

  • data是数据域，用于存放数据
  • prior是前驱指针域，存放该结点的前驱结点地址
  • next是后继指针域，存放该结点的后继结点地址

对于所有的操作都必须考虑前驱节点和后继节点，对他们共同操作！

总结

链表是最重要的数据结构基础，上面是我根据过往学习资料整理出来的一些知识点，希望能对未来有所帮助！！

阶段总结

数据结构的知识点是我一直以来都想总结的，也是未来必须需要的，文笔还是需要改进，代码还算是原创，是仿照之前的代码慢慢写出来的，整整两天时间，最终写完还算心情舒畅吧，马上就要启程去实习了，为了未来，加油！！！